Wesley Girls’ Core Mathematics Mock Questions

Wesley Girls’ Core Mathematics Mock Questions

Wesley Girls’ core mathematics mock questions: This core mathematics mock questions is designed by the one of the best schools in the country to enable their candidates pass with distinction.

see also: GSTS social studies mock questions and answers

see also: GSTS Geography mock questions paper 1,2&3

Core mathematics mock questions: Part I: [40 marks]

Answer all the five questions in this part. All questions carry equal marks.

1. a. Make y the subject of the relation: m/(n−y) = n/(m+y)

b. A boy has to cover 4km to catch a bus. He walks part of the distance at 3km/h and runs the rest at 5lm/h. If he takes 1 hour to complete the distance, how many kilometres does he walk?

2. a. Factorize: X² + ax – x – a

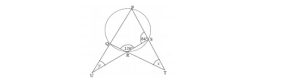
b. In the diagram, PQRS is a cyclic quadrilateral. /PS/ and /QR/ are produced to meet at T. /SR/ and /PQ/ are produced to meet at U. If and , find the values of x and y.

Core mathematics mock questions

3. The probability of two candidates A and B, passing an examination are 2/3 and 3/4 respectively. Find the probability that:

a. only one candidate will pass;

b. at least one candidate will pass.

Core mathematics mock questions

4. Two cyclists left a point at the same time. The first cyclist covered 300m on a bearing of 296° and the second cyclist covered 250m on a bearing of 206°. Calculate, correct to three significant figures:

a. the distance between the two cyclists;

b. the bearing of the second cyclist from the first.

Core mathematics mock questions

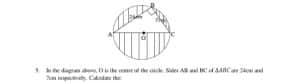
5. In the diagram above, O is the centre of the circle. Sides AB and BC of are 24cm and 7cm respectively. Calculate the:

a. radius of the circle;

b. area of the shaded portion, correct to the nearest whole number. (Take pie = 22/7)

PART II: [60 marks]

Answer five questions only from this part. All questions carry equal marks.

6. a. Using a ruler and a pair of compasses only, construct:

i. triangle PQR such that |PQ| = 8.5cm, ∠QPR = 60°and |PR| = 7.5cm;

ii. the locus l1 of points equidistant from P and R;

iii. the locus l2 of points equidistant from Q and R;

iv. locate the point of intersection I, of the loci l1 and l2.

b. i. Construct a circle passing through the three vertices of the triangle PQR.

ii. Find the radius of the circle.

iii. Measure |QR|.

Core mathematics mock questions

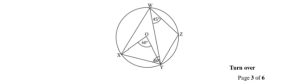
7. a. In the diagram, WXYZ are points on the circumference of a circle O , ∠XYW = 80°. Calculate , ∠ZYW.

b. A tank 2m tall stands on top of a concrete pillar. From a point (P) on the same horizontal ground as the foot of the pillar, the angles of elevation of the top (T) and bottom (B) of the tank are 49° and 42° respectively.

i. Draw a diagram to represent this information;

ii. Calculate, correct to one decimal place, the height of the pillar;

iii. Calculate, correct to one decimal place, |PB|.

Core mathematics mock questions

8. a. Using a scale of 2cm to 2 units on each axis, draw on a sheet of graph paper two perpendicular axes Ox and Oy, for the interval −10 ≤ x ≤ 10 and − 10 ≤ y ≤ 10.

b. Draw on the same graph sheet, indicating clearly the coordinates of all the vertices,

(i). the quadrilateral ABCD with coordinates A(2, 4), B(4, 7), C(8, 8) and D(6, 3).

(ii). the image A1B1C1D1 of quadrilateral ABCD under an anticlockwise rotation of 90° about the origin,

where A → A1, B → B1, C → C1 and D → B1.

(iii). the image A2B2C2D2 of quadrilateral ABCD under a translation by the vector

−10
−9

where A → A2, B → B2, C → C2 and D → D2

c. Find C1C2

Core mathematics mock questions

9. a. Copy and complete the table of values for the relation y = 2sinx + 1

b. Using scales of 2 cm to 30° on the x-axis and 2 cm to 1 unit on the y-axis,

draw the graph of y = 2sinx + 1 for 0° ≤ x ≤ 270°.

c. Use the graph to find the values of x for which sinx = 1/4

10. a. If 3/((2p−(1/2)) = 1/3((1/4p) +1)), find p.

b. A television set was marked for sale at GH¢760.00 in order to make a profit of 20%. The television set was actually sold at a discount of 5%. Calculate, correct to 2 significant figures, the actual percentage profit.

c. Solve (x − 2)(x − 3) = 12.

Core mathematics mock

11. a. (i) Illustrate the following statement in a Venn diagram: All good Literature students in a school are General Arts class.

(ii) Use the diagram to determine whether or not the following are valid conclusions from the given statement:

(α) Vivian is in the General Arts class therefore she is a good Literature student;

(β) Audu is not a good Literature student therefore he is not in the General Arts class;

(γ) Kweku is not in the General Arts class therefore he is not a good Literature student.

b. The cost (c) of producing n bricks is the sum of a fixed amount, h, and a variable amount y where y varies directly as n. If it costs GH¢ 950.00 to produce 600 bricks and GH¢ 1030.00 to 1000 bricks,

(i) find the relationship between c, h and n;

(ii) calculate the cost of producing 500 bricks.

Mathematics mock questions

12. The table shows the distribution of 40 students in a class according to their clubs and the corresponding sectoral angles.

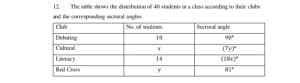
a. Find the value of x and y.

b. Illustrate the data on a pie chart.

c. Find the percentage of students who were in the cultural club.

Core mathematics mock questions

13. a. The diagram shows a rectangle PQRS from which a square of side x cm has been cut. If the area of the shaded portion is 484cm2, find the value of x.

b. (i). Draw a multiplication ⨂ table for the arithmetic modulo 7.

(ii). Using your table,

I. Evaluate (4 ⨂ 6) ⊗ (5 ⊗ 4)

II. Find the truth set of n⨂n = n